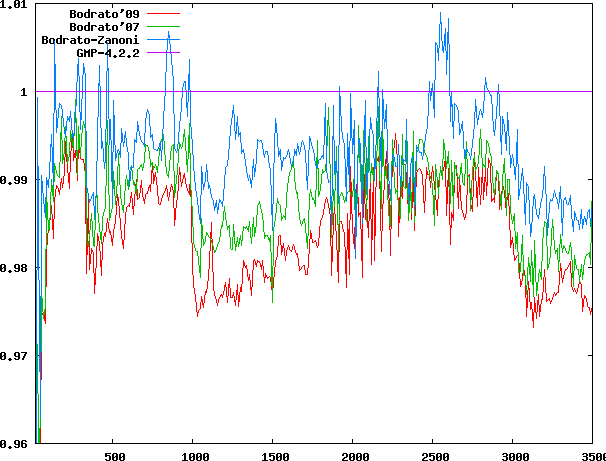
 Relative time for squaring
Relative time for squaringImplements the proven optimal (in a restricted but reasonable
model[1]) inversion sequence for
Toom-Cook 3x3, a shift less compared to current GMP[3]
code, and no temporaries. For processors without a native addlsh1
implementation, Bodrato'07[2] uses
also a proven optimal evaluation sequence, formulas can be also found
on the Toom-Cook optimal formulas page.
On my laptop (Centrino) the proposed code shows a slight
speed-up. Timing graphs are normalised with respect to
GMP-4.2.2. Bodrato-Zanoni code uses the new inversion,
Bodrato'07 uses both optimisations.
Latest code Bodrato'09 introduces a new unpublished trick to avoid half an operation.
Behaviour can be deeply different on different architectures, particularly those which have native addlsh1. If you try the
code and obtain much different results, please let us know:
Bodrato-Zanoni
<>.
Licence: GNU GPLv3+.
Download: gmp-4.2.2/mpn/generic/mul_n.c. (and a patch which can be applied to gmp-impl.h)
References: [1]What
About Toom-Cook Matrices Optimality? by Marco Bodrato and
Alberto Zanoni
[2]Towards Optimal Toom-Cook Multiplication for Univariate and Multivariate Polynomials in Characteristic 2 and 0 by Marco Bodrato
[3]GMP - The GNU Multi Precision library
Implements the proven optimal (in a restricted but reasonable model[1]) inversion sequence for Toom-3.5 (4x3 and 5x2). Some further optimisation are applied: adaptatation to "gmp[3] instruction set", and a final saving of an operation by interlacing interpolation and recomposition phases. Some optimisation are present also in the evaluation phase[2].
Licence: GNU GPLv3+.
Download: toom3_5_mul.c.
References: [1]What
About Toom-Cook Matrices Optimality? by Marco Bodrato and
Alberto Zanoni
[2]Towards Optimal Toom-Cook Multiplication for Univariate and Multivariate Polynomials in Characteristic 2 and 0 by Marco Bodrato
[3]GMP - The GNU Multi Precision library
Implements a new experimental strategy, mixing evaluation, interpolation and recomposition phases, to reduce the memory footprint and the linear complexity.
Two versions are available, the first one evaluating in {1,2,4} using exact division by 3 and by 45, the second one evaluating in {1/2,1,2} with divisions by 9 and by 15.
Licence: GNU GPLv3+.
Download: toom4.5 eval in 1,2,4, toom4.5 eval in 1/2,1,2.
References: None yet.
Implements a new experimental strategy, mixing evaluation, interpolation and recomposition phases, to reduce the memory footprint and the linear complexity.
All unbalanced evaluations are condensed in a single function. This
means that the function mpn_toom6h_mul implements both Toom-6
and Toom-6.5; i.e. 6x6, 7x6, 7x5, 8x5, 8x4 and 9x4. But 9x3, 10x3,
10x2 and 11x2 are not implemented at all.
The function
mpn_toom8h_mul implements both Toom-8 and Toom-8.5; i.e. 8x8,
9x8, 9x7, 10x7, 10x6, 11x6 and 11x5; on 64-bits CPU it implements also
12x5, 12x4 and 13x4. But 13x3, 14x3, 14x2 and 15x2 are not implemented
at all.
A squaring functions are given too, skiping the evaluation at infinity.
WARNING! Dont trust the _itch functions! The functions are almost NAILS-ready but has never been tested…
Licence: GNU GPLv3+.
Download: toom6.5_31ott2009.tbz; toom8.5_31ott2009.tbz.
References: High degree Toom'n'half for balanced and unbalanced multiplication by Marco Bodrato.
Graphs above where obtained on my laptop (Centrino) comparing a developement version of GMP, and MPIR Version 1.3.0-rc1. Both compiled with ./configure && make, without tuning.
All the three graphs shows the value: "cycles used for a multiplication"/"number of limbs^{3/2}", limbs are 32-bits long.
Observations:
It is quite hard to understand which one of the many unbalanced Toom is faster for a given couple of operands. To start investigation I produced a table reporting the fastest Toom-NxM algorithm present in (future versions of) GMP.
Download: toom.fastest-flavour.dvi.bz2 (DVI).
Some concrete experiments on Toom 4x4, 5x5, 6x6, 7x7, and 4x3-5x2
(Toom3.5), 5x3 (with Toom4) algorithms. The code for interpolation was
semi-automatically generated, with comments indicating limits every
variable value is between, as an indication for mpn optimisation, none
of the implemented method was proven optimal though.
Graphs refer to code executed on my laptop (Centrino), with speedups
around 20% for balanced and around 35% for unbalanced, for
middle-sized integers.
Licence: GNU GPLv3+.
Download: GMP implementation of Toom-Cook 5, 6, 7, and 3.5 as a tar bzip2 file.
References:
Towards Optimal Toom-Cook Multiplication for Univariate and Multivariate Polynomials in Characteristic 2 and 0 by Marco Bodrato
GMP implementation of
Toom-Cook 4 by Paul Zimmermann
What About Toom-Cook Matrices
Optimality? by Marco Bodrato and Alberto Zanoni
Implements the same sequences as above, within the LibTomMath
environment. On my laptop this patch obsoletes the Karatsuba
multiplication, it gives in fact:
KARATSUBA_MUL_CUTOFF = 128
TOOM_MUL_CUTOFF = 129
Not the same for squaring, where the tuning suggests:
KARATSUBA_SQR_CUTOFF = 128
TOOM_SQR_CUTOFF = 186
The original library was included by many projects, but it seems that
it is not maintained any more… Let me know if you need a patch for your
project, probably with a different licence.
Licence: GNU GPLv3+.
Download: libtommath/bn_mp_toom_mul.c, libtommath/bn_mp_toom_sqr.c.
References: [1]What
About Toom-Cook Matrices Optimality? by Marco Bodrato and
Alberto Zanoni,
[2]Towards Optimal Toom-Cook Multiplication for Univariate and Multivariate Polynomials in Characteristic 2 and 0 by Marco Bodrato.